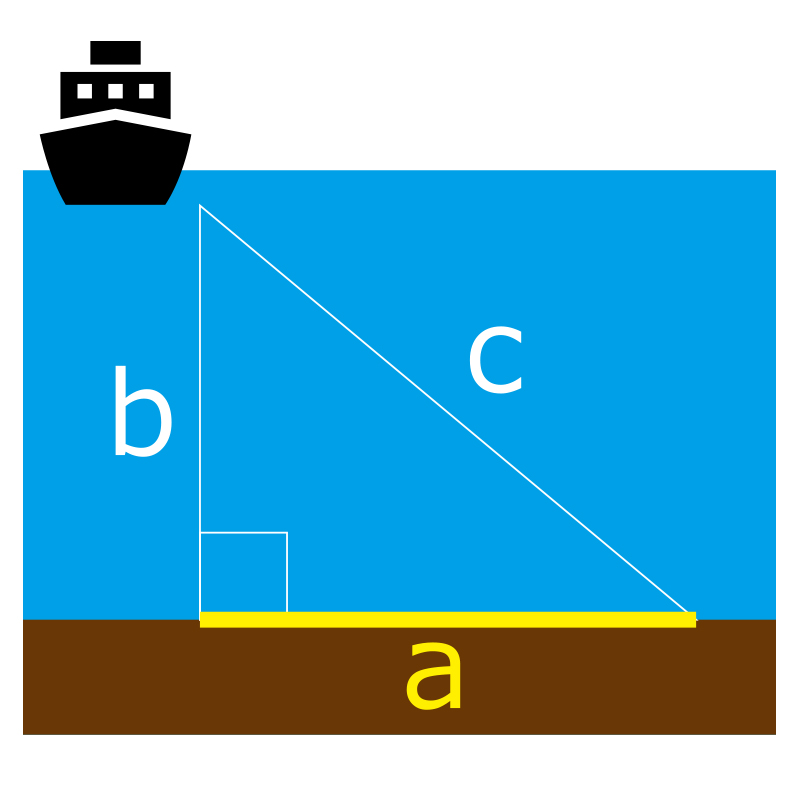
仕事で三角形の1辺の長さを求める必要となり、どんな計算式だったかなと思い出すより数値を入れるだけで計算してくれるサイトを見つける方が早い時代ですね（笑）

求めたかったのは、直角三角形でbとcの長さが分かる時、aの長さはってなやつです。いとも簡単に計算してくれて仕事が捗りました。

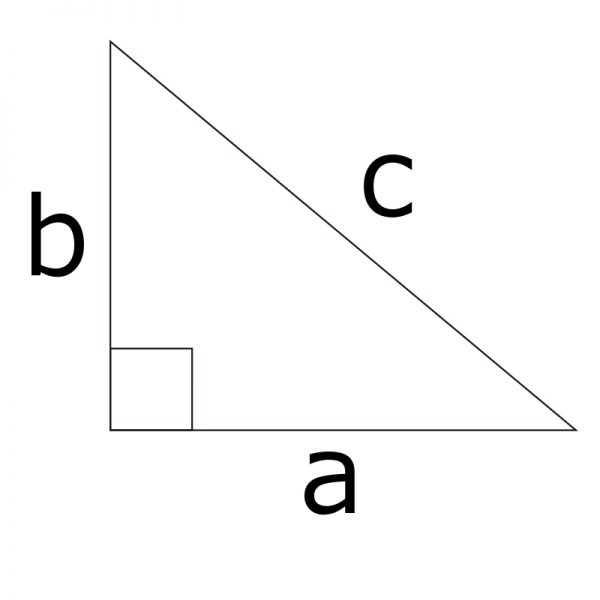
ん？

これって・・・。

こうしたら・・・（笑）

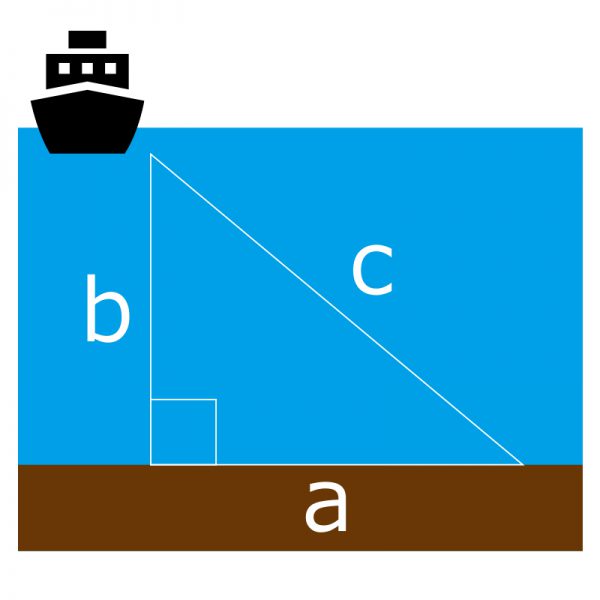
ドテラ流しになりました!!

そうです、「c」はカウンター付きリールがのライン放出量、「b」は水深です。

水深100mのところでラインが120m放出されていたら、船の真下からどれくらい離れたところから巻き上げているんだろう？そう言えば自分の感覚では、水深100mのところでラインが120m放出されたくらいでは、そんなに離れているイメージはないが、どれくらいと言われたら答えられませんでした。

計算してみましょう！

※机上の理論です。実際は、潮の流れでラインが直線になっていないので、以下で述べていることは正確な値ではありません。参考程度にどうぞ。

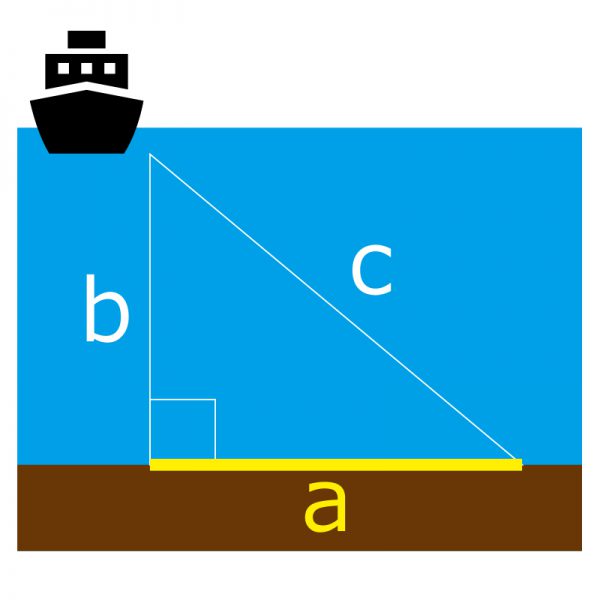
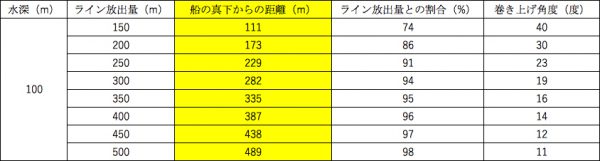
ラインの放出量が多くなればなるほど、船の真下から鯛ラバまでの距離は、ラインの放出量に近づいていきますね

数字にしてみると驚きでした。ラインの放出量が多ければ多いほど、ロッドの角度とラインの角度が平行になる理由もうなずけますね。船から離れている距離を把握する必要はないですけど、イメージとして把握しておくのは悪くないかもしれません。しかしこんな数字覚えるの大変ですよね。そこで、リールのカウンター（ラインの放出量）からイメージできるようにしました。

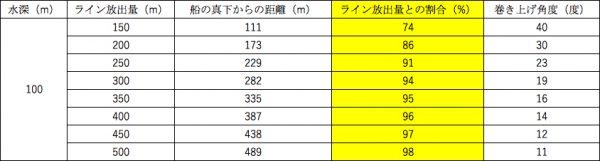
すごくざっくりですが、水深100mのところなら

150mの放出量でおおよそ7割、200mで8割、300mで9割

と覚えておけばよいのではないでしょうか。

次に巻き上げる角度です。

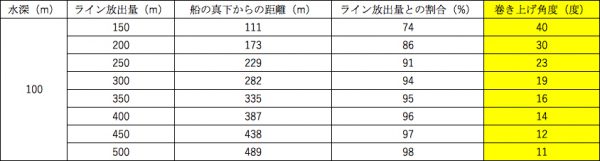
150m放出された場合で40度、300mで20度、450mで10度

と覚えておけばよいのではないでしょうか。

あまり飛ばさない方が釣れる、かなり先まで飛ばした方が釣れるというのは、この角度もキモになっているのかもしれませんね。

海の中ではラインがまっすぐではなくフケているでしょうから正確な値ではありませんが、知らないより、おおよその数値でも知っておく方が、ディープドテラがより楽しいものになるのではないでしょうか。

釣りに行けない時は、こんな想像をしてああでもない、こうでもないと考える時間が楽しいもの。

暖かい日が多くなり、出かけるのが楽しく気持ちよい季節。

想像したことが正しいかどうか、フィールドへ答え合わせしにいきましょ！